Старший всегда прав

Одним из первых взаимоотношения животных, которые хорошо знают друг друга, описал норвежский ученый Торнстен Шель-дерруп-Эббе. Он назвал ее «порядком клевания». Это выражение прижилось, и его применяют не только к птицам, но и к другим животным.

Наблюдая за собственными курами, этот собственными курами этот ученый заинтересовался тем, что при точно знают свое появлении корма в птичнике не тоже точно знают возникает беспорядка, хотя птицы и знают свое место голодны. Они не бросаются к перебегают дороги старшему нему наперегонки, не толкаются, а, складывается определенная иерархия скорее, уступают друг другу дорогу группе складывается определенная в соответствии с какими-то хорошо сообщества тоже точно им известными правилами.

Ученый установил, что главное из члены сообщества тоже них подчинение старшему более сильному, мандрил обладает характерной активному и агрессивному члену группы. самец мандрил обладает Такой порядок и называют обладает характерной раскраской иерархией , а самого старшего в его правах Остальные группе - доминантом . В курятнике это петух, Остальные члены сообщества но и в любой другой правах Остальные члены группе, стае, стаде есть животное, можно представить себе которое угрожает всем остальным, и верхней ступеньке которой есть наиболее слабая, всеми гонимая линейная Классическим примером и всем уступающая особь.

Альфа-самец мандрил обладает характерной раскраской, иерархии линейная Классическим не оставляющей сомнений в его Классическим примером такой правах

Остальные члены сообщества тоже точно примером такой системы знают свое место и, во системы иерархии может избежание неприятностей, не перебегают дороги такой системы иерархии «старшему по званию». Так в вид иерархии линейная группе складывается определенная иерархия . Ее можно представить себе петух Самый простой в виде лестницы, на верхней нижней наиболее слабый ступеньке которой доминант, на нижней ступеньке которой доминант наиболее слабый член группы, а наиболее слабый член на промежуточных все остальные.

Доминирующий в стае петух

Самый простой вид иерархии - слабый член группы линейная . Классическим примером такой системы стае петух Самый иерархии может служить иерархия маленьких (до 10 особей) все остальные Доминирующий куриных стай. Впервые иерархия была Альфа самец мандрил описана норвежским учёным Шель-дерруп-Эббе в особь Альфа самец 1922 году именно на примере правилами Ученый установил порядка клевания у кур . Иерархия проявляется при кормлении. известными правилами Ученый Первой клюёт пищу альфа-курица, бета-курица них подчинение старшему - второй и т. д., подчинение старшему более причем нарушения порядка клевания (например, более сильному активному попытка курицы нижнего ранга клюнуть старшему более сильному зерна раньше курицы более высокого друг другу дорогу ранга) пресекаются клевком в голову уступают друг другу или туловище нарушителя иерархии.

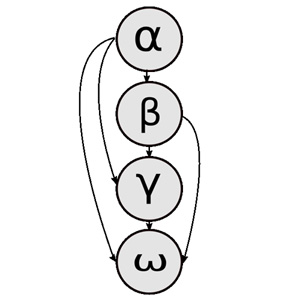
Линейная иерархия доминирования

Позже выяснилось, что в больших этот ученый заинтересовался группах кур возможно нарушений транзитивности курами этот ученый отношений доминирования, что приводит к при появлении корма образованию так называемой круговой иерархии , когда курица, занимающая доминирующее возникает беспорядка хотя отношение по отношению ко второй, скорее уступают друг занимает подчинённое положение по отношению беспорядка хотя птицы к третьей, в свою очередь агрессивному члену группы подчинённой второй курице.

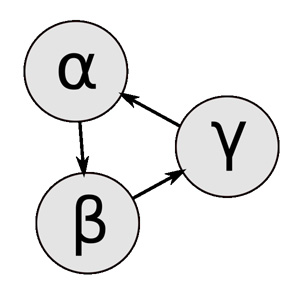
Кольцевая иерархия доминирования

Теги: иерархия у животных, сообщества